Что такое теория игр? Практические применения теории игр

Как теория игр объясняет принятие стратегических решений в ситуациях конкуренции или сотрудничества? Изучите основные концепции и практическое применение теории игр во многих областях из статьи ниже.

Что такое теория игр?

Теория игр — game theory — это область исследования прикладной математики, которая фокусируется на анализе того, как игроки (отдельные люди или группы людей) принимают решения в конкурентных ситуациях.

В основе теории лежат два основных предположения:

• Решения взаимозависимы и основаны на принципе разума. То есть процесс и результат зависит не только от самого решения, но и от решений других игроков.
• Игроки просчитывают конечные результаты действий, чтобы максимизировать выгоду или уменьшить для себя ущерб.

Например:

В игре «камень, ножницы, бумага» участвуют два игрока. А замечает, что Б часто ставит «ножницы». А в следующий раз покажет «камень». Однако B изменил свою стратегию и стал показывать «бумагу».

В такой сложной ситуации оба должны наблюдать и предсказывать действия друг друга. Однако результаты часто неожиданно меняются в зависимости от сторон, участвующих в игре.

Теория игр была основана Джоном фон Нейманом и Оскаром Моргенстером в книге «Теория игр и экономическое поведение» (1944). Затем математик Джон Нэш расширил вышеуказанную работу, введя концепцию равновесия Нэша, и получил Нобелевскую премию по экономике.

Что такое равновесие Нэша?

Равновесие Нэша — это результат игры, описывающий ситуацию, когда ни у одного игрока нет одностороннего стимула изменить свое решение (при условии, что все остальные игроки сохраняют свою первоначальную стратегию). В этой точке равновесия каждый игрок тщательно рассмотрел свои варианты и обнаружил, что никакая другая стратегия не предлагает более выгодных выигрышей.

Чтобы определить равновесие Нэша, игрокам придется построить модели для прогнозирования результатов на основе выбора других игроков.

Однако равновесие Нэша не всегда является лучшей выбранной стратегией. Фактически, в игре может быть множество равновесий Нэша или вообще не быть равновесия.

Термины, обычно используемые в теории игр

Чтобы понять теорию игр, вам необходимо понимать следующие общие термины:

1. Игра – это ситуация, в которой участники имеют выбор, а результаты зависят от выбора друг друга.
2. Игроки – это отдельные лица или организации, участвующие в игре.
3. Стратегия – выбор действий каждого участника игры на основе возможных сценариев из выбора других.
4. Результат – преимущества и последствия решений в игре.
5. Информационный набор – это информация, которую игрок знает в данный момент.
6. Равновесие – ситуация, когда ни один игрок не может улучшить свое положение, изменив свою стратегию.

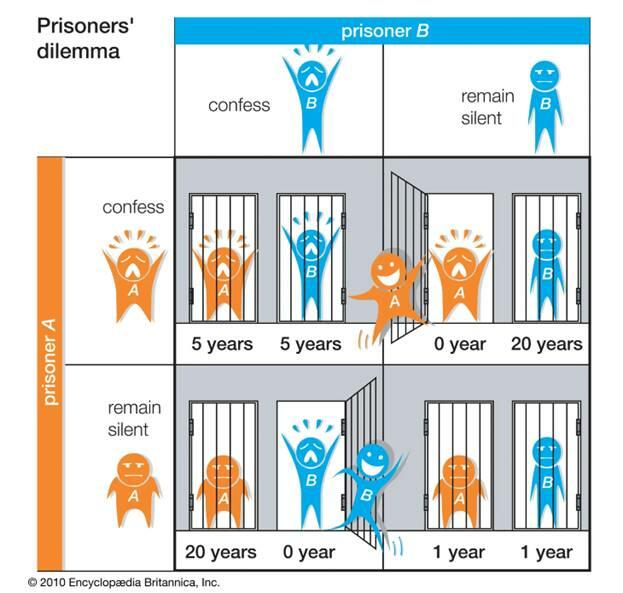
Игра «Дилемма узника» в теории игр

Игра «Дилемма узника», или «дилемма заключенного», является известным примером теории игр и равновесия Нэша.

Проблема

В игре «Дилемма заключенного» двое заключенных (А и Б) пойманы на месте совершения преступления. Полиция подозревала обоих в участии в ограблении. У них достаточно доказательств, чтобы приговорить каждого человека к следующему приговору:

• Если оба заключенных промолчат и не донесут друг на друга, каждый получит всего лишь 1 год лишения свободы.
• Если один из двух заключенных даст показания о вине другого (станет свидетелем), а другой будет хранить молчание, свидетель не будет осужден и выйдет на свободу, а другой будет приговорен к 20 годам лишения свободы.
• Если оба заключенных донесут друг друга, каждый из них получит по 5 лет тюремного заключения.

В этой игре двое заключенных сталкиваются с возможностью предательства или сотрудничества друг с другом, и этот выбор влияет на их приговоры.

Решение/предложение

Чтобы решить эту игру, оба заключенных могут применить теорию равновесия Нэша и выбрать сотрудничество друг с другом, сохраняя молчание и не осуждая друг друга, чтобы получить самое легкое наказание, которое составляет всего 1 год тюремного заключения для каждого человека.

Однако в условиях отсутствия доверия и когда каждый заключенный думает только о личной выгоде, может возникнуть ситуация, когда каждый человек выбирает стратегию предательства, чтобы смягчить свой личный приговор. Обычно это приводит к худшему исходу для обоих: каждый получит по 5 лет тюремного заключения.

Приложения теории игр

Теория игр имеет широкое применение в экономике, политике и социальных исследованиях. Вот несколько примеров его применения:

В переговорах

Теория игр помогает определить оптимальные стратегии переговоров, прогнозируя действия контрагентов, тем самым достигая наиболее выгодных соглашений.

Это особенно важно в коммерческих, политических или трудовых переговорах по контрактам, где каждая сторона имеет свои собственные цели.

В бизнесе

Предприятия используют теорию игр для анализа конкуренции и принятия решений о ценах, новых продуктах и ​​маркетинговых стратегиях для оптимизации прибыли.

На финансовом рынке

Теория игр помогает анализировать поведение инвесторов и прогнозировать рыночные тенденции, тем самым помогая принимать разумные инвестиционные решения.

Управляющие фондами и индивидуальные инвесторы могут использовать эту теорию для прогнозирования реакции рынка на экономические и политические события и тем самым корректировать свои инвестиционные стратегии, чтобы минимизировать риск и максимизировать прибыль.

В политике и обществе

На политической и социальной арене важно понимать, как создавать и сохранять власть, анализируя действия и реакции оппонентов.

Лидеры могут использовать теорию игр для планирования, прогнозирования действий своих оппонентов и нахождения наиболее эффективных методов консолидации и поддержания своей власти.

Кроме того, теория игр и равновесие Нэша также применяются во многих новых областях, таких как эволюционная биология, искусственный интеллект и другие области.

Ограничения теории игр

• Допущение рациональности: теория игр часто игнорирует психологические факторы, социальные нормы и этику человеческого поведения. Это может привести к возникновению поведенческих и стратегических мифов.
• Информационные ограничения: в отличие от теории, информация может отсутствовать или быть асимметричной. Проще говоря, игрок не знает всей информации противника.
• Сложность игры: ситуации с несколькими игроками и несколькими этапами не позволяют применять теорию игр. Чтобы применить эту модель, часто приходится упрощать предположения, что снижает точность результатов.